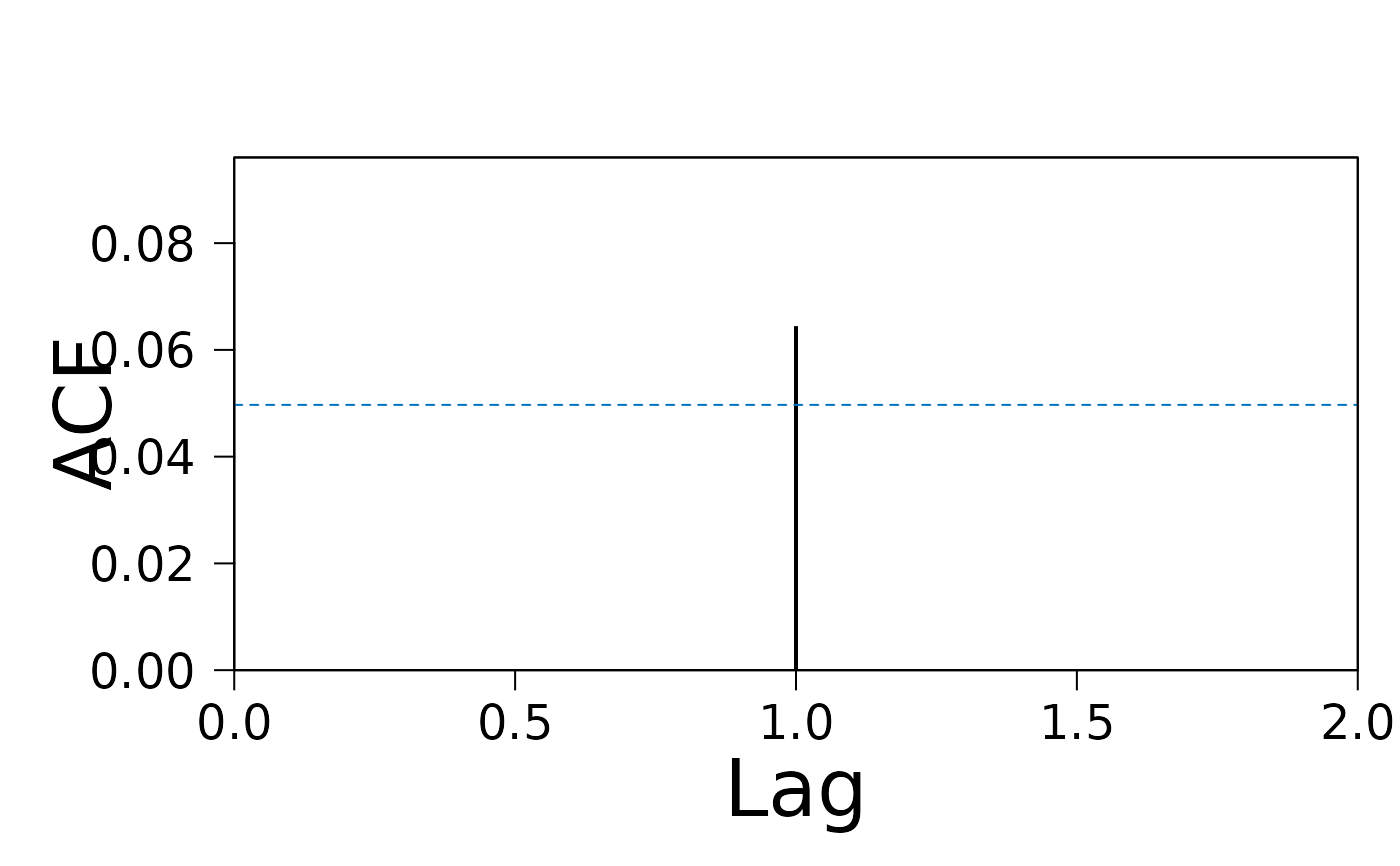Skip to contents

ACF/PACF Functions

acf.Rd

This function computes the ACF/PACF of data. This can be applied on traditional scalar time series or functional time series defined in dfts().

Usage

acf(x, lag.max = NULL, ...)

# Default S3 method
acf(x, lag.max = NULL, ...)

pacf(x, lag.max = NULL, ...)

# Default S3 method
pacf(x, lag.max = NULL, ...)

# S3 method for class 'dfts'
acf(
  x,
  lag.max = NULL,
  alpha = 0.05,
  method = c("Welch", "MC", "Imhof"),
  WWN = TRUE,
  figure = TRUE,
  ...
)

# S3 method for class 'dfts'
pacf(x, lag.max = NULL, n_pcs = NULL, alpha = 0.95, figure = TRUE, ...)

Arguments

x

Object for computation of (partial) autocorrelation function (see acf() or pacf).

lag.max

Number of lagged covariance estimators for the time series that will be used to estimate the (partial) autocorrelation function.

...

Further arguments passed to the .plot_FACF function.

alpha

A value between 0 and 1 that indicates significant level for the confidence interval for the i.i.d. bounds of the (partial) autocorrelation function. By default alpha = 0.05.

method

Character specifying the method to be used when estimating the distribution under the hypothesis of functional white noise. Accepted values are:

  • "Welch": Welch approximation.

  • "MC": Monte-Carlo estimation.

  • "Imhof": Estimation using Imhof's method.

By default, method = "Welch".

WWN

Logical. If TRUE, WWN bounds are also computed

figure

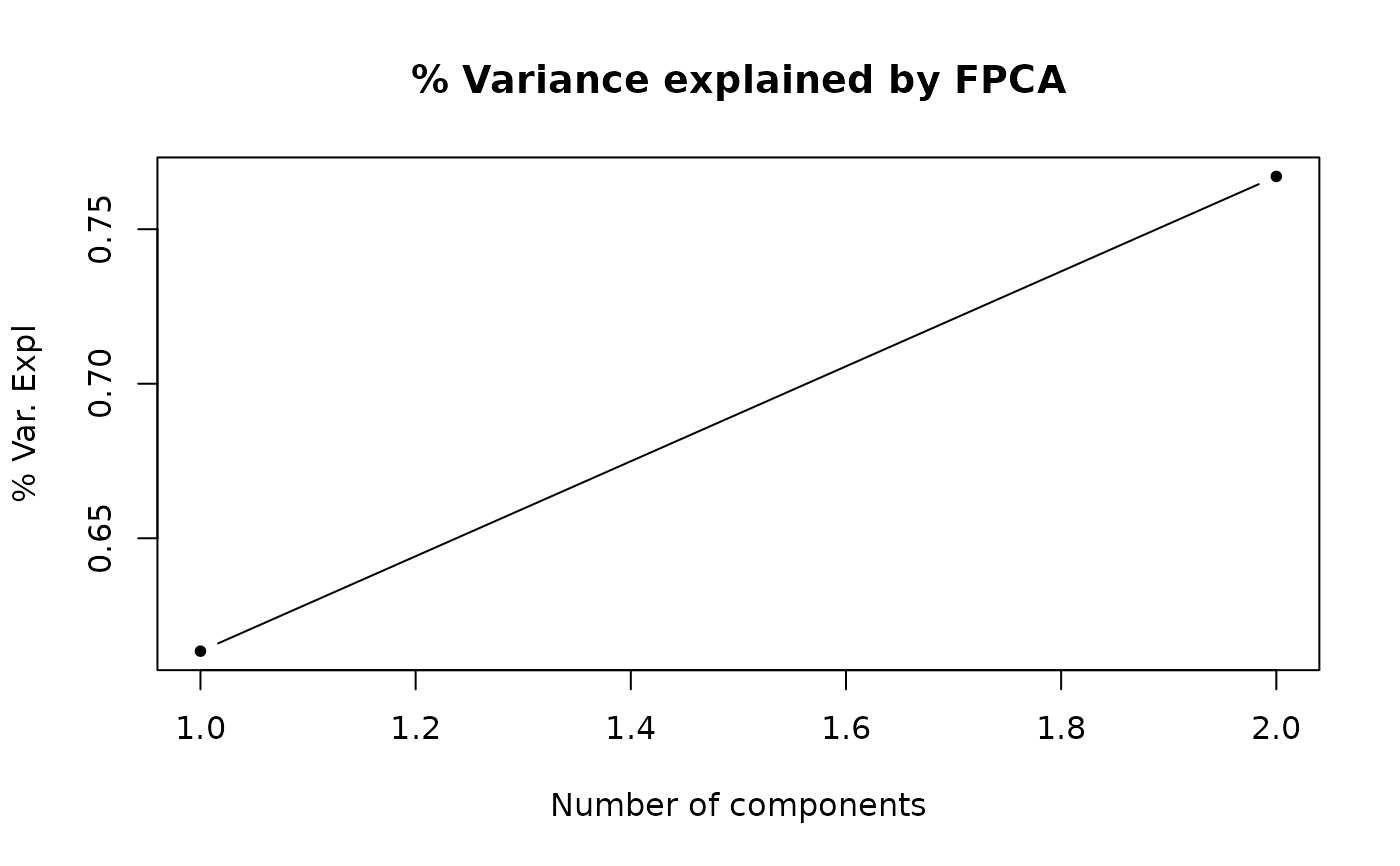
Logical. If TRUE, plots the estimated function with the specified bounds.

n_pcs

Number of principal components that will be used to fit the ARH(p) models.

Value

List with ACF or PACF values and plots

  • acfs/pacfs: Autocorrelation values for each lag of the functional time series.

  • SWN_bound: The upper prediction bound for the i.i.d. distribution under strong white noise assumption.

  • WWN_bound: The upper prediction bound for the i.i.d. distribution under weak white noise assumption.

  • plot: Plot of autocorrelation values for each lag of the functional time series.

References

Mestre G., Portela J., Rice G., Munoz San Roque A., Alonso E. (2021). Functional time series model identification and diagnosis by means of auto- and partial autocorrelation analysis. Computational Statistics & Data Analysis, 155, 107108.

Mestre, G., Portela, J., Munoz San Roque, A., Alonso, E. (2020). Forecasting hourly supply curves in the Italian Day-Ahead electricity market with a double-seasonal SARMAHX model. International Journal of Electrical Power & Energy Systems, 121, 106083.

Kokoszka, P., Rice, G., Shang, H.L. (2017). Inference for the autocovariance of a functional time series under conditional heteroscedasticity Journal of Multivariate Analysis, 162, 32–50.

See also

stats::acf()

Examples

acf(1:10)

x <- generate_brownian_bridge(100, seq(0,1,length.out=20))
acf(x,20)


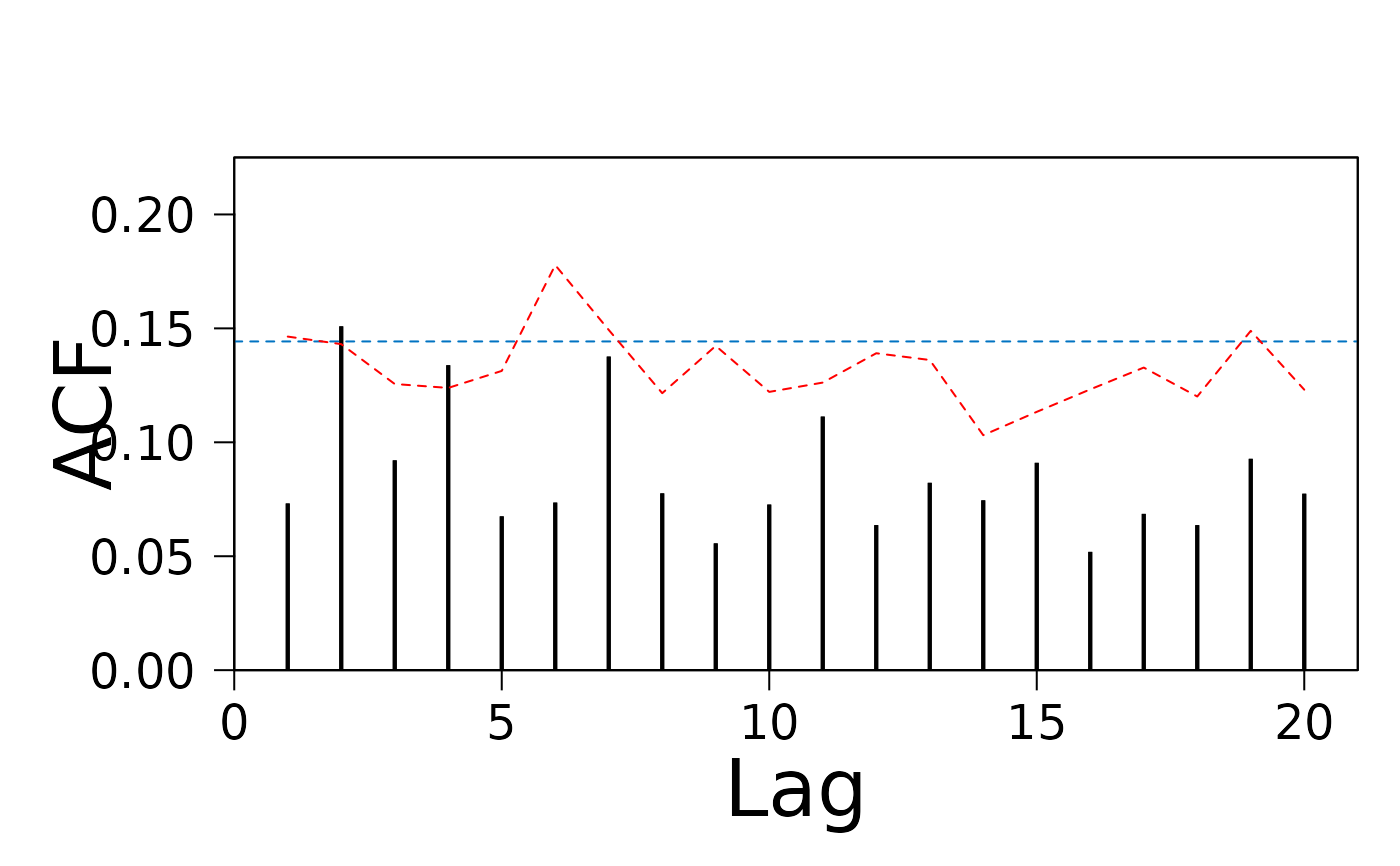x <- generate_brownian_bridge(100, seq(0,1,length.out=20))
pacf(x,lag.max = 10, n_pcs = 2)